Giới thiệu
Kiểm định t một mẫu được sử dụng để xác định xem một mẫu có đến từ một quần thể có giá trị trung bình cụ thể hay không. Giá trị trung bình của quần thể này không phải lúc nào cũng được biết, nhưng đôi khi được đưa ra giả thuyết.
Ví dụ, hãy tưởng tượng một học giả đang tiến hành nghiên cứu về mối quan hệ giữa kết quả thi và thời gian ôn tập, nhưng trước tiên muốn kiểm tra xem 100 người tham gia của mình có phản ánh đúng mức trung bình toàn quốc về năng lực học tập, được đo bằng điểm GMAT hay không. Học giả có thể sử dụng kiểm định t một mẫu để so sánh điểm GMAT của 100 người tham gia với mức trung bình toàn quốc. Hoặc, hãy tưởng tượng một giảng viên tin rằng khóa học của cô ấy yêu cầu 10 giờ học mỗi tuần và muốn xác định xem sinh viên có dành đủ thời gian này để học hay không. Giảng viên có thể sử dụng kiểm định t một mẫu để so sánh thời gian học hàng tuần của một mẫu gồm 20 sinh viên với 10 giờ được đề xuất.
Trong hướng dẫn này, chúng tôi sẽ hướng dẫn bạn cách thực hiện kiểm định t một mẫu bằng Minitab, cũng như cách diễn giải và báo cáo kết quả kiểm định này. Tuy nhiên, trước khi giới thiệu quy trình này, bạn cần hiểu các giả định khác nhau mà dữ liệu của bạn phải đáp ứng để kiểm định t một mẫu cho kết quả hợp lệ. Chúng ta sẽ thảo luận về các giả định này ở phần sau.
Minitab
Giả định
Kiểm định t một mẫu có bốn giả định. Bạn không thể kiểm định hai giả định đầu tiên trong số này bằng Minitab vì chúng liên quan đến thiết kế nghiên cứu và lựa chọn biến của bạn. Tuy nhiên, bạn nên kiểm tra xem nghiên cứu của mình có đáp ứng hai giả định này hay không trước khi tiếp tục. Nếu những giả định này không được đáp ứng, có thể bạn sẽ cần một kiểm định thống kê khác để thay thế. Giả định số 1 và số 2 được giải thích dưới đây:
- Giả định #1: Biến phụ thuộc của bạn phải được đo ở mức liên tục (tức là, đó là một biến khoảng hoặc biến tỷ lệ ). Ví dụ về các biến liên tục bao gồm chiều cao (đo bằng feet và inch), nhiệt độ (đo bằng °C), lương (đo bằng đô la Mỹ), thời gian sửa đổi (đo bằng giờ), trí thông minh (đo bằng điểm IQ), quy mô công ty (đo theo số lượng nhân viên), độ tuổi (đo bằng năm), thời gian phản ứng (đo bằng mili giây), lực nắm (đo bằng kg), công suất đầu ra (đo bằng watt), hiệu suất kiểm tra (đo từ 0 đến 100), doanh số bán hàng (đo bằng số giao dịch mỗi tháng), thành tích học tập (đo theo điểm GMAT), v.v. Nếu bạn không chắc chắn liệu biến phụ thuộc của mình có liên tục hay không (tức là, được đo ở mức khoảng hoặc tỷ lệ), hãy xem hướng dẫn Các loại biến của chúng tôi .
- Giả định #2: Dữ liệu độc lập (tức là không tương quan/liên quan ), nghĩa là không có mối quan hệ nào giữa các quan sát. Đây là vấn đề về thiết kế nghiên cứu hơn là một vấn đề bạn có thể kiểm tra, nhưng đây là một giả định quan trọng của kiểm định t một mẫu.
Giả định #3 và #4 liên quan đến bản chất dữ liệu của bạn và có thể được kiểm tra bằng Minitab. Bạn cần kiểm tra xem dữ liệu của mình có đáp ứng các giả định này không, vì nếu không, kết quả bạn nhận được khi chạy kiểm định t một mẫu có thể không hợp lệ. Trên thực tế, đừng ngạc nhiên nếu dữ liệu của bạn vi phạm một hoặc nhiều giả định này. Điều này không phải là hiếm. Tuy nhiên, có những giải pháp khả thi để khắc phục những vi phạm đó (ví dụ: chuyển đổi dữ liệu) để bạn vẫn có thể sử dụng kiểm định t một mẫu. Giả định #3 và #4 được giải thích dưới đây:
- Giả định #3: Không nên có giá trị ngoại lệ đáng kể . Giá trị ngoại lệ chỉ đơn giản là một trường hợp trong tập dữ liệu của bạn không tuân theo quy luật thông thường. Ví dụ, hãy xem xét một nghiên cứu kiểm tra mức độ lo lắng khi làm bài kiểm tra của 500 học sinh, trong đó mức độ lo lắng được đo lường trên thang điểm từ 0-100, với 0 = không lo lắng và 100 = mức độ lo lắng tối đa. Điểm lo lắng trung bình khi làm bài kiểm tra là 56 và đại đa số học sinh đạt từ 42 đến 70. Tuy nhiên, có một học sinh chỉ đạt 2 điểm trên thang điểm, với điểm lo lắng thấp thứ hai là 36. Do đó, một học sinh chỉ đạt 2 điểm trên thang điểm "có thể" được coi là giá trị ngoại lệ. Khi điểm số là giá trị ngoại lệ, điều này gây ra vấn đề vì giá trị ngoại lệ có thể có tác động tiêu cực không cân xứng đến kiểm định t một mẫu, làm giảm độ chính xác của kết quả. May mắn thay, khi sử dụng Minitab để chạy kiểm định t một mẫu trên dữ liệu của bạn, bạn có thể dễ dàng phát hiện các giá trị ngoại lệ tiềm ẩn.
- Giả định #4: Biến phụ thuộc của bạn phải có phân phối chuẩn . Chúng ta đang nói về kiểm định t một mẫu chỉ yêu cầu dữ liệu xấp xỉ chuẩn vì nó khá "mạnh" đối với các vi phạm chuẩn, nghĩa là giả định có thể bị vi phạm một chút mà vẫn cho kết quả hợp lệ. Bạn có thể kiểm tra tính chuẩn bằng kiểm định chuẩn Shapiro-Wilk, có thể dễ dàng kiểm tra bằng Minitab.
Trên thực tế, việc kiểm tra các giả định #3 và #4 có thể sẽ chiếm phần lớn thời gian của bạn khi thực hiện kiểm định t một mẫu. Tuy nhiên, đây không phải là một nhiệm vụ khó khăn, và Minitab cung cấp tất cả các công cụ bạn cần để thực hiện việc này.
Trong phần Quy trình Kiểm định trong Minitab , chúng tôi minh họa quy trình Minitab cần thiết để thực hiện kiểm định t một mẫu với giả định không có giả định nào bị vi phạm. Trước tiên, chúng tôi trình bày ví dụ được sử dụng để giải thích quy trình kiểm định t một mẫu trong Minitab.
Minitab
Ví dụ
Một nhà nghiên cứu dự định tiến hành một nghiên cứu để xác định ba loại điều trị khác nhau ảnh hưởng đến trầm cảm như thế nào. Tuy nhiên, trước khi thực hiện nghiên cứu này, nhà nghiên cứu muốn đảm bảo rằng 40 người tham gia có điểm trầm cảm được coi là "bình thường". Hãy tưởng tượng rằng điểm 4,0 được coi là phản ánh mức độ trầm cảm "bình thường". Điểm thấp hơn cho thấy mức độ trầm cảm thấp hơn và điểm cao hơn cho thấy mức độ trầm cảm cao hơn. Do đó, mức độ trầm cảm của tất cả 40 người tham gia được đo lường và kiểm định t một mẫu được sử dụng để xác định xem mẫu này có đại diện cho một quần thể bình thường hay không (tức là, liệu điểm trung bình của quần thể ước tính theo mẫu có khác biệt đáng kể so với 4,0 hay không). Điểm trầm cảm được ghi lại trong biến, Điểm trầm cảm .
Minitab
Thiết lập trong Minitab
Trong Minitab, chúng tôi thiết lập biến phụ thuộc, Điểm trầm cảm , trong cột 
. Sau đó, chúng tôi nhập điểm của biến phụ thuộc (tức là điểm trầm cảm của từng người tham gia) vào 
cột. Điều này được minh họa bên dưới:
Được xuất bản với sự cho phép bằng văn bản của Minitab Inc.
Lưu ý: Nếu bạn không có đầy đủ dữ liệu cho biến phụ thuộc của mình, không giống như ví dụ trên, mà chỉ có dữ liệu được tóm tắt (tức là kích thước mẫu, giá trị trung bình và độ lệch chuẩn), bạn sẽ cần thiết lập dữ liệu theo cách khác.
Minitab
Quy trình kiểm tra trong Minitab
Trong phần này, chúng tôi sẽ hướng dẫn bạn cách phân tích dữ liệu bằng kiểm định t một mẫu trong Minitab khi bốn giả định trong phần trước, Giả định , không bị vi phạm. Do đó, ba bước cần thiết để chạy kiểm định t một mẫu trong Minitab được trình bày dưới đây:
- Nhấp vào Thống kê cơ bản > 1 - Mẫu t... trên menu trên cùng, như hiển thị bên dưới:
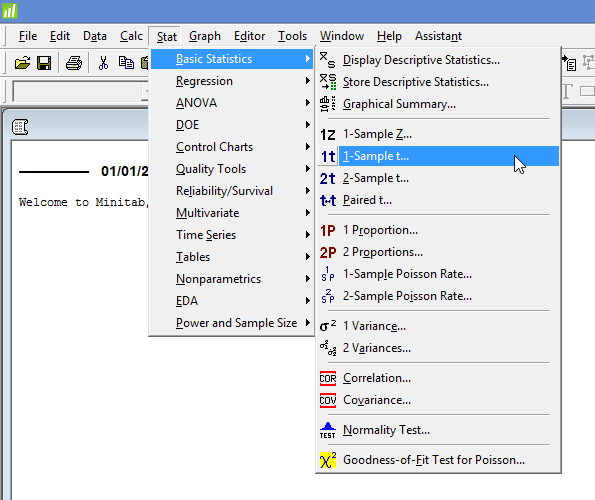
Được xuất bản với sự cho phép bằng văn bản của Minitab Inc.
Bạn sẽ thấy hộp thoại 1-Mẫu t (Kiểm định và Khoảng tin cậy) sau :
Được xuất bản với sự cho phép bằng văn bản của Minitab Inc.
- Giữ nguyên tùy chọn Mẫu theo cột và nhập biến phụ thuộc, Điểm trầm cảm , vào ô bên dưới. Bạn sẽ thấy hộp thoại như hình dưới đây:
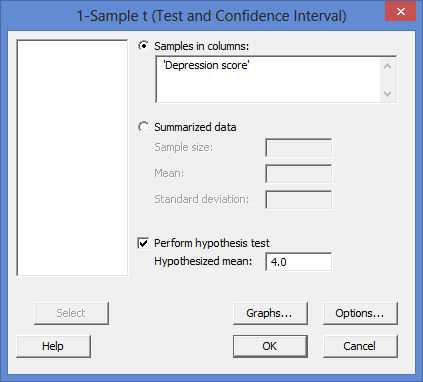
Được xuất bản với sự cho phép bằng văn bản của Minitab Inc.
Giải thích: Để chuyển biến phụ thuộc, Điểm trầm cảm , trước tiên bạn cần nhấp vào ô Mẫu theo cột: để biến phụ thuộc xuất hiện trong ô chính bên trái (ví dụ: Điểm trầm cảm C1 ). Thao tác này sẽ kích hoạt
nút (thường mờ: 
). Tiếp theo, chọn Điểm trầm cảm C1 , sau đó nhấn nút hoặc chỉ cần nhấp đúp vào Điểm trầm cảm C1 .Lưu ý 1: Theo mặc định, Minitab sử dụng khoảng tin cậy 95%, tương đương với việc khai báo ý nghĩa thống kê ở mức p < .05. Nếu bạn muốn thay đổi, trước tiên bạn có thể nhấp vào
nút, hộp thoại Tùy chọn t - 1 mẫu sẽ mở ra , như được hiển thị bên dưới: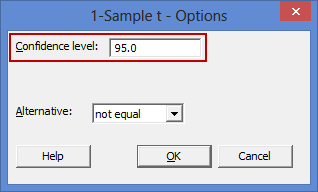
Để thay đổi giá trị của khoảng tin cậy, chỉ cần nhấp vào hộp Mức tin cậy: – được tô sáng màu đỏ ở trên – và thay đổi giá trị (ví dụ: giá trị 99,0 sẽ tương đương với việc khai báo ý nghĩa thống kê ở mức p < .01).Lưu ý 2: Ngoài quy trình trên, còn có một phương pháp khác để thực hiện kiểm định t một mẫu trong Minitab (được tô sáng trong hình chữ nhật màu đỏ bên dưới).
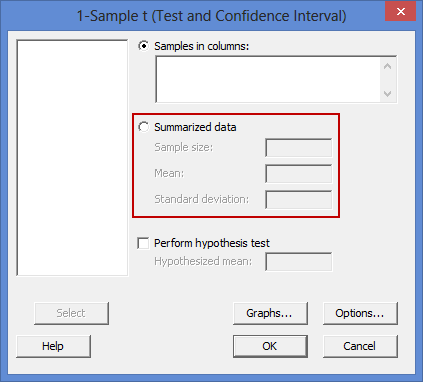
Phương pháp thay thế này hữu ích nếu bạn chỉ có dữ liệu tóm tắt (ví dụ: kích thước mẫu, giá trị trung bình và độ lệch chuẩn cho biến phụ thuộc), thay vì tất cả các điểm. - Nhấp vào
nút. Kết quả đầu ra mà Minitab tạo ra được hiển thị bên dưới.
Minitab
Đầu ra của bài kiểm tra t một mẫu trong Minitab
Đầu ra Minitab cho bài kiểm tra t một mẫu được hiển thị bên dưới:
Bạn sẽ được trình bày các số liệu thống kê mô tả bao gồm kích thước mẫu (cột " N "), giá trị trung bình (cột " Mean "), độ lệch chuẩn (cột " StDev ") và sai số chuẩn của giá trị trung bình (cột " SE Mean "), cũng như khoảng tin cậy (CI) 95% của giá trị trung bình ( CI 95% ). Cuối cùng, kết quả của kiểm định t một mẫu bao gồm giá trị trung bình quần thể đã biết hoặc giả định mà bạn đang so sánh với dữ liệu mẫu ( hàng Kiểm định mu = 4 so với not = 4 ), giá trị t quan sát được (cột " T ") và ý nghĩa thống kê (giá trị p hai đuôi ) của kiểm định t một mẫu (cột " P ").
Trong ví dụ của chúng tôi, bạn có thể thấy giá trị điểm trầm cảm 'bình thường' là "4" (Kiểm định mu = 4 so với không = 4 hàng). Kích thước mẫu ( N ) là 40, điểm trầm cảm trung bình ( Mean ) là 3,723, với độ lệch chuẩn là 0,737, và khoảng tin cậy 95% của giá trị trung bình là từ 3,487 đến 3,958. Giá trị t quan sát được ( T ) là -2,38 và mức ý nghĩa thống kê là 0,022. Bậc tự do là 39, nhưng điều này không được hiển thị trong kết quả đầu ra của Minitab (Lưu ý, đây chỉ đơn giản là kích thước mẫu, N , trừ 1; do đó 40 – 1, bằng 39). Do đó, có thể kết luận rằng các giá trị trung bình của quần thể khác biệt có ý nghĩa thống kê.
Lưu ý: Chúng tôi trình bày kết quả từ kiểm định t một mẫu ở trên. Tuy nhiên, vì bạn đã kiểm định dữ liệu của mình cho các giả định mà chúng tôi đã giải thích trước đó trong phần Giả định , bạn cũng sẽ cần diễn giải kết quả đầu ra của Minitab được tạo ra khi bạn kiểm định chúng. Kết quả này bao gồm: (a) các biểu đồ hộp bạn đã sử dụng để kiểm tra xem có bất kỳ giá trị ngoại lai đáng kể nào không; và (b) kết quả đầu ra mà Minitab tạo ra cho kiểm định chuẩn Shapiro-Wilk của bạn để xác định tính chuẩn. Ngoài ra, hãy nhớ rằng nếu dữ liệu của bạn không đáp ứng bất kỳ giả định nào trong số này, kết quả đầu ra mà bạn nhận được từ quy trình kiểm định t một mẫu (tức là kết quả đầu ra mà chúng tôi đã thảo luận ở trên) có thể không còn hợp lệ nữa, nhưng bạn có thể sử dụng một kiểm định thống kê khác thay thế.
Minitab
Báo cáo kết quả của bài kiểm tra t một mẫu
Khi bạn báo cáo kết quả của bài kiểm tra t một mẫu, bạn nên bao gồm:
- A. Giới thiệu về phân tích bạn đã thực hiện.
- B. Thông tin về mẫu của bạn ( N ).
- C. Một tuyên bố về việc liệu kiểm định t một mẫu có ý nghĩa thống kê hay không, bao gồm giá trị trung bình ( Mean ) và độ lệch chuẩn ( StDev ), khoảng tin cậy 95% của giá trị trung bình ( 95% CI ), giá trị t ( T ), bậc tự do và mức ý nghĩa, hay cụ thể hơn là giá trị p 2 đuôi ( P ).
Dựa trên kết quả đầu ra của Minitab ở trên , chúng tôi có thể báo cáo kết quả của nghiên cứu này như sau:
- Tổng quan
Kiểm định t một mẫu đã được thực hiện để xác định xem điểm trầm cảm của người tham gia có khác với điểm bình thường hay không, được định nghĩa là điểm trầm cảm là 4,0. Điểm trầm cảm trung bình (3,72, 95% CI, 3,49 đến 3,96) thấp hơn điểm trầm cảm bình thường là 4,0, một sự khác biệt có ý nghĩa thống kê, t (39) = -2,83, p = 0,022.
